Simple Distribution Problem
This example is taken from the MOOC MITx: CTL.SC2x (edX plateform). You can check the MOOC for more information about mathematical programming and the implementation with excel.
In this post, I propose an implementation using Gurobi Python environment.
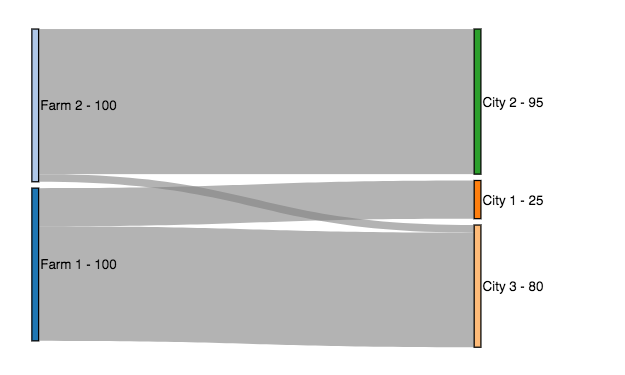
Following Sankey diagram represents the solution to this problem.
Input data
\(S_{i} : \text{production of tomatoes from each Farm i (in tons)}\) \(D_{j} : \text{demand from each City j (in tons)}\) \(c_{i,j} : \text{transportation cost between Farm i and City j (€/ton)}\)
Decision variables
\(x_{i,j} : \text{flow on arc between Farm i to City j}\)
Input Data
\(S_{1} = 100\) \(S_{2} = 125\) \(D_{1} = 25\) \(D_{2} = 95\) \(D_{3} = 80\) \(C_{1,1} = 250\) \(C_{1,2} = 325\) \(C_{1,3} = 445\) \(C_{2,1} = 275\) \(C_{2,2} = 260\) \(C_{2,3} = 460\)
Objective
Minimisation of the transportation cost
\[\min \sum\limits_{i \in{I}}\sum\limits_{j\in{J}} x_{i,j} * c_{i,j}\]Supply constraint
Production of each farm cannot exceed the sum of the deliveries to all the cities.
\[\sum\limits_{j\in{J}} x_{i,j} \leq S_{i} \qquad \forall i \in I\]Demand constraint
Demand of each city must be satisfied : one city can be delivered by two farms.
\[\sum\limits_{i\in{I}} x_{i,j} \geq D_{j} \qquad \forall j \in J\]Non negativity constraint
\[x_{i,j} \geq 0 \qquad \ \forall i,j\]Implementation in Python
from gurobipy import *
farms = ["Farm1", "Farm2"]
cities = ["City1", "City2", "City3"]
supply = { "Farm1" : 100,
"Farm2" : 125}
demand = { "City1" : 25,
"City2" : 95,
"City3" : 80}
cost = { "Farm1" : { "City1" : 250,
"City2" : 325,
"City3" : 445},
"Farm2" : { "City1" : 275,
"City2" : 260,
"City3" : 460}}
m = Model("transportation_pb")
# Decision variables
flow = m.addVars(farms, cities, name="flow")
# Supply constraint
supply_constr = m.addConstrs((flow.sum(farm, "*")
<= supply[farm] for farm in farms),
name="supply_constraint")
# Demand constraint
demand_constr = m.addConstrs((flow.sum("*", city)
>= demand[city] for city in cities),
name="supply_constraint")
# Objective function
obj = quicksum(flow[farm, city] * cost[farm][city]
for farm in farms
for city in cities)
m.setObjective(obj, GRB.MINIMIZE)
m.optimize()
| Tons of tomatoes delivered | |
| Farm1 | 25.0 tons to City1 0.0 tons to City2 75.0 tons to City3 |
| Farm2 | 0.0 tons to City1 95.0 tons to City2 5.0 tons to City3 |
The total cost is 66 625 €.
How can we improve our business ?
for c in m.getConstrs():
print(c.ConstrName, c.slack)
>>> supply_constraint[Farm1] 0.0
>>> supply_constraint[Farm2] 25.0
>>> supply_constraint[City1] 0.0
>>> supply_constraint[City2] 0.0
>>> supply_constraint[City3] 0.0
The farm 2 still has 25 tons of unsold tomatoes.